PHP nasıl bir trend çizgisi hesaplayabilirsiniz?

1 Cevap php

Yani bir grafik için bir trend çizgisi hesaplanması için ilgili iki soru okudum, ama ben yine kayboldum.

Ben xy koordinatları bir dizi var, ve ben PHP kullanarak bir logaritmik eğilim çizgisini temsil xy koordinatları başka dizi (daha az koordinatlar olabilir) ile gelmek istiyorum.

Ben istemci tarafında grafik çizmek için javascript bu dizileri geçiyorum.

1 Cevap

Logarithmic Least Squares

Biz log x değerleri alarak bir çizgi içine bir logaritmik fonksiyon dönüştürebilirsiniz yana, biz bir linear least squares eğri uydurma gerçekleştirebilirsiniz. Aslında, iş bizim için yapılmış ve bir çözüm Math World yer almaktadır.

Kısaca, biz $X ve y = a + b * log(x) gibi bir dağıtım vardır $Y değerleri verilen konum. En küçük kareler yöntemi, bazı değerleri aFit vermek ve bFit verilen veri noktalarına parametrik eğri mesafeyi en aza indirecektir.

Here is an example implementation in PHP:

Önce $a ve $b tarafından verilen bilinen yatan dağılımı ile bazı rasgele verileri oluşturmak olacak

  // True parameter valaues
  $a = 10;
  $b = 5;

  // Range of x values to generate
  $x_min = 1;
  $x_max = 10;
  $nPoints = 50;

  // Generate some random points on y = a * log(x) + b
  $X = array();
  $Y = array();
  for($p = 0; $p < $nPoints; $p++){
    $x = $p / $nPoints * ($x_max - $x_min) + $x_min;
    $y = $a + $b * log($x);

    $X[] = $x + rand(0, 200) / ($nPoints * $x_max);
    $Y[] = $y + rand(0, 200) / ($nPoints * $x_max);

  }

Şimdi, burada $a ve $b tahmin verilen denklemleri nasıl kullanacağınız.

  // Now convert to log-scale for X
  $logX = array_map('log', $X);

  // Now estimate $a and $b using equations from Math World
  $n = count($X);
  $square = create_function('$x', 'return pow($x,2);');
  $x_squared = array_sum(array_map($square, $logX));
  $xy = array_sum(array_map(create_function('$x,$y', 'return $x*$y;'), $logX, $Y));

  $bFit = ($n * $xy - array_sum($Y) * array_sum($logX)) /
          ($n * $x_squared - pow(array_sum($logX), 2));

  $aFit = (array_sum($Y) - $bFit * array_sum($logX)) / $n;

Daha sonra yoğun olarak sizin gibi Javascript için puan oluşturabilir:

  $Yfit = array();
  foreach($X as $x) {
    $Yfit[] = $aFit + $bFit * log($x);
  }

Bu durumda, kod tahminleri bFit = 5.17 ve aFit = 9.7, sadece 50 veri noktaları için oldukça yakın olan.

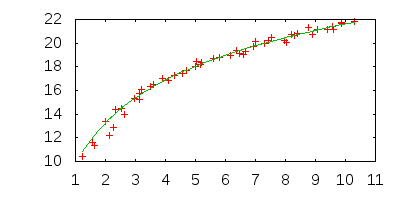
alt text

Aşağıdaki açıklamada verilen örnek veriler için, logaritmik bir fonksiyon iyi uymuyor.

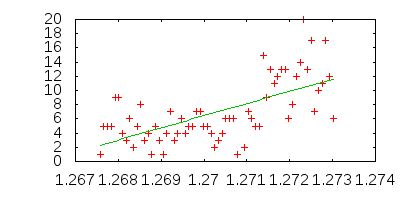
alt text

En küçük kareler çözümü aslında bu alanda bir çizgidir y = -514.734835478 + 2180.51562281 * log(x) hangi.

etiketler